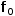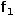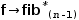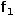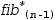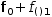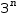9.4 Serial tuples

A serial tuple is a tuple value that contains definitions and a single value item. The value item is the last item in the tuple. The type of a serial tuple is the type of the value item.

Evaluation of a serial tuple occurs in a new scope. Before evaluation, definitions are bound and the value item is then bound to names contributed by the definitions (or to non-local names). The result of evaluating a serial tuple is the result of evaluating the value item. During evaluation, contributing definitions are memoized upon reference. The idea of serial tuples is similar to that found in several programming languages, sometimes known as a “serial clause”. The scope of definitions is confined to the tuple.

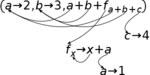
For example, (a→1, b→2, a+b) evaluates to 3; (f(x)→x^2, (f(x)|x∈0, 3)) evaluates to (0, 1, 4, 9).

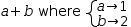
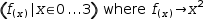
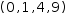
Figure 9.12 shows the bindings for a serial tuple with both local and non-local bindings. Note in particular the two instances of variable a, one referenced from the value item and one referenced from a non-local function definition.

9.4.1 Fibonacci sequence

To illustrate a more complex use of a serial tuple, two techniques to find the n^th number in the Fibonacci sequence will be developed. The sequence starts with 1, 1 and continues by adding the last two numbers to obtain the next: 1, 1, 2, 3, 5, 8, 13, ... Thus fib(7) is 13 and is produced by fib(6)+fib(5).

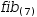
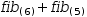
The first technique does not make use of a serial tuple but has a significant performance problem resulting from duplicate recursion. The piecewise function

satisfies the sequence, but performs an exponential number of function invocations, of order 2^n.

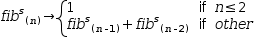
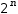
The second technique to improves the performance by using a serial tuple with a definition that captures the last two numbers of the sequence in a tuple and references that tuple to compute the next number. The piecewise function

illustrates the technique. Note the expressions fʈ[0] and fʈ[1] are not function calls, but indexes into the tuple bound to fʈ. Due to memoization, the expression fʈ→fib__*ʈ(n-1) is evaluated just once during each function activation. That value is used by any reference to fʈ in the same activation. Without memoization, evaluation of fʈ[1] would evaluate the elaboration fib__*(n-1) (recursively) before extracting the indexed item. This is followed by the two bindings in fʈ[0]+f()[1], leading to another two recursions. Without memoization, this version would be of order 3^n.